The radar equation represents the
physical dependences of the transmit power, the wave propagation up
to the receiving of the echo-signals. Furthermore can be assessed
the performance of radar sets with the radar equation.
Argumentation/Derivation
| At first we assume, that electromagnetic waves can
propagate with ideal conditions without disturbing
influences.
If high-frequency energy is emitted by an
isotropic radiator, than the energy propagate evenly to all
directions. Areas of same power density therefore form
spheres ( A= 4 π R� ) around the radiator. At incremented
spheric radius the same value of energy spreads out around
on an incremented spherical surface. That means: the power
density on an assumed area becomes lower with an increasing
distance of the radiator. |
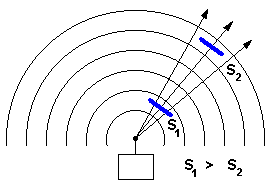 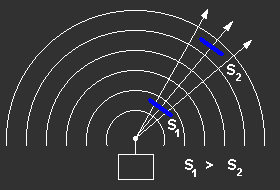
Figure 1: nondirectional power density |
So we get the formula to calculate
the Nondirectional Power Density Su
| Su = |
Ps |
in |
W |
|
|
| 4 � π � R12 |
m2 |
|
PS = transmitted power
[W]
SU = nondirectional power density
R1 = Range Antenna - Target [m] |
(1) |
If the irradiation is limited on a
spherical segment (at constant transmit power), then results an
increase of the power density in direction of the radiation. This
effect is called antenna gain. This gain is made by directional
irradiation of the power. For the directional power density apply:
Sg = Su � G
|
Sg = directional power density
G = antenna gain |
(2) |
Of course in the reality radar
antennas aren't �partially radiating� isotropic radiators. Radar
antennas have to have a small beam width and an antenna gain up to
30 or 40 dB. (e.g. parabolic dish antenna or phased array antenna).
The target detection isn't only
dependent on the power density at the target position. In addition
of this it depends by the reduction how much is back reflected
actually in direction of the radar equipment. To be able to
determine the utilizable reflected power, the value of the radar
cross section σ is needed. This difficultly comprehensible quantity
is dependent on several factors. It is that way plausibly at first,
a bigger area reflects more power than a little area. That means:
A Jumbo jet offers more radar cross
section than a sporting aircraft at same flight situation. Beyond
this the re-reflecting area depends on design, surface composition
and the using materials.
This is said summarized till now: At
the final destination the reflected power Pr arises from the power density Su, the antenna gain G and
the very variable radar cross section σ:
| Pr = |
Ps |
� G� σ in [W] |
|
| 4 � π � R12 |
|
Pr = reflected power
σ = radar cross section |
(3) |
| Simplified a target can be regarded as a
radiator in turn due to the reflected power. The reflected
power Pr then becomes the emitted power.
Since
there are the same conditions as on the way there on the way
back of the echos yields himself for the power density at
the receive place Se: |
Figure 2: Connection between
formula 3 and 4 |
| Se = |
Pr |
in |
W |
|
|
| 4 � π � R12 |
m2 |
|
Se = power density at
receive place
Pr = reflected power [W]
R2 = range antenna - target [m] |
(4) |
At the radar antenna the received
power is dependent on the power density at the receive place PE and the effective antenna area AW .
PE = Se � AW
|
PE = power density at the receive place
[W]
AW = effective antenna area [m�] |
(5) |
The effective antenna area arises
from the fact that an antenna doesn't work loss-freely i.e. the
geometric measurements are available not quite as a receive area. As
a rule, the effect of an antenna is smaller than these have
geometric measurements suspected around the factor 0.6 to 0.7
(Factor Ka).
Applies to the effective antenna
area:
AW = A � Ka
|
AW = effective antenna area [m�]
A = geometric antenna area [m�]
Ka = Factor |
(6) |
For the power at the receive place PE arises therefore:
The way there and way back was looked
at separately at the argumentation till now. With the next step both
ways being summarized: Since R2 (Target - Antenna) is the
distance R1 (Antenna - Target) at once, this is taken
into account now.
Another given equation (however, this
one shall not be derived in this place) puts the antenna gain G in
connection with the used wavelength λ.
This is convert to the antenna area A
and put into the upper equation. After the simplification it yields:
| Pe = |
Ps � G2 � σ � λ2 |
in [W] |
|
| (4 � π)2 �
R4 |
|
(11) |
After the converting to the range
R the classic form results for the radar equation:
All quantities which have influence on
the wave propagation of the radar signals were taken into account at
this radar equation. Beyond this the dependences of the sizes were
illustrated and summarized in the classic radar equation at least.
Until after this theoretical attempt can
be used the radar equation very well also in the practice e.g. to
determine the efficiency of radar sets. The form of the classic radar
equation isn't, however, suitable for these extended considerations yet.
Some further considerations are necessary.
Obtained on a given radar equipment most
sizes (Ps, G , λ) can be regarded as constant since they are
only in very little ranges variable parameters. Against this the radar
cross section represents a quantity to be described heavily and
therefore 1 m� is assumed as a practical oriented value mostly.
Under this condition that value of the
received power PE is interesting, which in the radar receiver
causes an even still visible signal. This received power is called PE
min. Smaller received powers aren't usable since they would lost
in the noise of the receiver. The occurred into the radar equation
received power PE min causes that with the equation the
theoretically maximum range Rmax can be calculated
now.
An application of this radar equation is
the determination of the performance of radar units to compare each
other.
Influences on the maximum range of a radar unit
All considerations in connection with the
radar equation were made under the prerequisite till now that the
electromagnetic waves can propagate under ideal conditions without
disturbing influences. In the practice a number of losses appears,
though. These cannot remain unconsidered since they partly reduce the
effectiveness of a radar unit considerably.
To this, at first the radar equation is
extended by the loss factor Lges.
This factor summarizes the following
listed kinds of losses:
- L D = internal
attenuation factors of the radar unit on the transmitting path and
the receive path
- L f = fluctuation losses
during the reflection
- L Atm = atmospheric
losses during the propagation of the electromagnetic waves in
direction of the target (and the way back)
Piece of internal losses arise in the
main thing at high frequency components, like waveguides, filters but
also by a radome. Obtained on a given radar unit this kind of loss is
relatively constant and also well measurable in it's value.
As permanent influence, still has to be
called the atmospheric attenuation and reflections at the earth's
surface.
Influence of the earth's surface
An extended, lesser-used form of the
radar equation considers additional factors, like the influence of the
Earth's surface and does not continue to classify receiver sensitivity
and the atmospheric absorption.
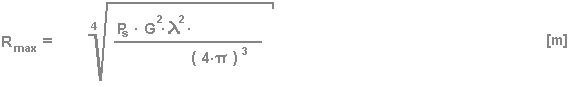
In this formula, in addition to the already well-known quantities:
| Kα= |
Dissipation factor in place of Lges. |
Az= |
effective reflection surface in place of σ |
| Ti= |
Pulse length |
K= |
Boltzmann's constant |
| T0= |
absolute Temperature in �K |
nR= |
Noise figure of the receiver |
| d= |
Clarity factor of the display terminal |
γ= |
Reflected beam angle |
| δR= |
Break-even factor |
Re= |
Distance of the absorbing medium |
The factor with the trigonometric
functions represents the influence of the Earth's surface. The earth
plane immediately surrounding a radar antenna has a significant impact
on the vertical polar diagram.
| By the combination of the direct with the reflected echo,
the transmitting and receiving patterns of the antenna change.
This influence is substantial in the VHF range and decreases
with increasing frequency. For the detection of targets at low
heights, a reflection at the Earth's surface is necessary. This
is possible only if the ripples of the area within the first
Fresnel zone do not exceed the value 0.01 R (i.e.: Within a
radius of 1000 m no obstacle may be larger than 1 m!). |
|
 |
Radar Reflections from Flat Ground
Specialised Radars at lower ( VHF-)
frequency band make use of the reflections at the Earth's surface and
lobing to maximise cover at low levels. At higher frequencies these
reflections are more disturbing. The following picture shows the lobe
structure caused by ground reflections. Normally this is highly
undesirable as it introduces intermittent cover as aircraft fly through
the lobes. The technique has been used in ATC ground mounted radars to
extend the range but is only successful at low frequencies where the
broad lobe structure permits adequate cover at higher elevations.
|
|
Free space vertical pattern
diagram |
| Effect of ground reflections |
| Gray, my dear friend, is every
theory: here it is the idealized cosecant squared- diagram! |
Raising the height of the antenna has the
effect of making the lobbing pattern finer. A fine grained lobing
structure is often filled in by irregularities in the ground plane.
Specifically, if the ground plane deviates from a flat surface then the
reinforcement and destruction pattern resulting from the ground
reflections breaks down. Avoidance of lobe effects is one of the prime
considerations when selecting a radar location and the height of the
antenna.
|





![]()